お前と、お前の知り合いがボタンを渡されてそれぞれ別々の部屋に入れられる
・トイレとベッドと相棒の部屋につながる電話だけが置いてある狭い部屋
・2人ともボタンを押さなければ翌朝部屋から解放される
・1人だけがそのボタンを押せば、押した方は翌朝大金をもらって解放され、押さなかった方は翌朝解放時間に死ぬ
・2人ともボタンを押せば、一生その部屋から出られない(食事は死ぬまで支給される)
ボタン押すか押さないか
押さない
>>3
せやね
宿題は自分でやれ
>>4
宿題じゃないよ俺が思いついたゲーム
まぁ囚人のジレンマをいじっただけだけど
知り合いがいない
俺死にたいから相手に押すように言って寝るわ
出られないのが一番怖いから幼い
死んでもラッキー
囚人のジレンマで支配戦略一個しかないから
相手が悩んでるうちにさっさと押した方がいい
>>10
あ、ボタンを押したその瞬間に相手が死ぬわけではないからね
押したら、翌朝の解放時間(例えば明朝8時)に押してない方が死ぬ
つまり、押したのに、電話で「2人で部屋から出ような!俺は絶対に押さないぞ!」とか演技できる
暖房とか全部完備されてんの?
>>13
そうだね室温は一生適温としよう
大金が一生豪遊できるレベルなら躊躇なく押す
知り合いが誰を選んでも押しそうだから押す
死ぬか部屋から出られないか、どっちのほうが嫌かで変わるやん
利得を
大金をもらって解放される…+10
解放される…0
一生部屋から出られない…-5
死ぬ…-10
としたら、
・相手が押す場合
→自分も押す…-5
→押さない…-10
・相手が押さない場合
→自分は押す……+10
→押さない…0
よって「押す」のが合理的ではある
>>21
まずその利得の数字がどこから出てくるのかを教えてくれないとな
個人的には一生部屋から出られないのは-100くらいあるんだけど
>>26
まぁ、それは個人差だわな
部屋から出られないのが死ぬよりキツイって人もいるのか
人間って難しいな…
電話で脱獄の相談するわ
相手を騙せそうかどうかで選択を変えるケースもあるじゃん
両方とも合理的なアクターであるなら絶対に二人とも押す結果になる
紛争や対立における戦略的局面を数学的に解析しようとする試みは、19世紀以前より行われていた。そして、それらの考えを体系的に整理した人物としては、当時の測度論の権威であったエミール・ボレルの名が知られている。フォン・ノイマンは、それらの試みにさらなる理論的意味付けを与え、理論体系を構築し、1928年には『ゲーム理論(Zur Theorie der Gesellschaftsspiele)』を、また1937年には『均斉成長経路の定式化とブラウワーの定理の一般化(Uber ein okonomisches Gleichungssystem und eine Verallgemeinerung des Brouwerschen Fixpunksatzes)』発表した。これらの論文では、「対象モデルをコンパクト凸集合として扱い、それに対してブラウワーの不動点定理を適用する」という現在のゲーム理論における主流ともいえる手法がすでに用いられていた。1928年の『ゲーム理論』でミニマックス定理の証明がなされたことで、ゲーム理論の応用数学としての枠組みが明確化されるようになった。しかし、これらの論文は、不動点定理を経済学の均衡問題に適用すると言う点で斬新ではあったものの、数学的には目新しい要素はなく、理論の適用対象となるモデルも限定されており、かつ用途も分かりにくいものであったため、大きく取り上げられることはなかった。
その後、ノイマンは、経済学者のオスカー・モルゲンシュテルンと共に、ゲーム理論を経済学の世界へと持ち込み、1944年に『ゲーム理論と経済行動(Theory of Games and Economic Behavior)』を共著で発表した。この論文では、経済的に紛争状態にある諸主体とその利害関係、不完全情報、合理的決定、偶然などの因子の存在についての分析から始まるものであり、実際的な情勢は理論的に定式化できるゲームにモデル化されている。この活動は、ジョン・ナッシュ、ラインハルト・ゼルテン、ジョン・ハーサニ、ロバート・オーマン、トーマス・シェリング、ロイド・シャープレー、ジョン・メイナード=スミスなど、数学的慧眼を持つ若者達を引きつけ、ゲーム理論は学問の世界で次第に広がった。
20世紀半ばのゲーム理論研究の中心地は、1948年に米空軍の研究機関として創設されたランド研究所であった。ランド研究所では、ゲーム理論に力学系や集合論、離散数学、組合せ最適化等の手法を取り入れる試みが行われ、これらによってゲーム理論は飛躍的な発展を遂げた。
後にリーマン多様体の研究に関して大きな功績を残す数学者ジョン・ナッシュは、プリンストン大学の博士課程在学中に非ゼロ和ゲームについて研究を行った。ナッシュは、角谷静夫による角谷の不動点定理を一般化し、「n人有限ゲームには、最低でも一つの均衡点、つまりプレーヤーが相互に最適な戦略を取り合って手を変えない状態(ナッシュ均衡)が存在すること」を証明した。これは、非零和ゲームに均衡点が存在することを明らかにした意味で、画期的な発見であった。
1950年代には、ハロルド・クーンらによって、完全情報や行動戦略などの概念が定義され、完全情報ゲームにおける均衡点の存在と完全情報ゲームでの行動戦略と混合戦略が同値であることが証明された。また、協力ゲームにおける安定集合の存在を踏まえ、ロイド・シャープレーによって、一般n人協力ゲームにおける代表的な解であるシャープレイ値が明らかにされた。
1950年、アメリカ合衆国ランド研究所のメリル・フラッドは、人間の不合理性をゲーム理論の方法で解明する研究を進め、ナッシュの均衡理論に反するような不合理な行動に着目した。ナッシュ均衡点の解とは、後からゲームを振り返って、双方が自分の戦略に満足できる選択肢の組合せである。フラッドは、メルヴィン・ドレッシャーと共同して、現実の人間の行動を観察する実験研究を行った。そして、フラッド・ドレッシャー実験の結果から、「被験者がナッシュ均衡点である行動はむしろ稀である」ことを報告した。また、同じくランド研究所の顧問であったアルバート・タッカーは、この実験結果を紹介するために、よく知られている囚人のジレンマの物語を作り上げた。囚人のジレンマでは、全体の利得に反して、個々人の利得を最大化せざるをえないことを示唆していた。同時に、これは、ゲーム理論が単一のミニマックス、ナッシュ均衡に基づいて戦略を立案する合理的プレーヤーの存在について見直しを要請する結果でもあった。
https://ja.wikipedia.org/wiki/ゲーム理論
そうなんだよね
それがナッシュ均衡ってやつ
これに似たゲームを実際に志願者募ってやってみたいな
軽い報酬と軽い罰ゲームくらいにしたら倫理的にも許されそうな実験だし
ゲーム理論における非協力ゲームの解の一種であり、いくつかの解の概念の中で最も基本的な概念である。数学者のジョン・フォーブス・ナッシュにちなんで名付けられた。
ナッシュ均衡は、他のプレーヤーの戦略を所与とした場合、どのプレーヤーも自分の戦略を変更することによってより高い利得を得ることができない戦略の組み合わせである。ナッシュ均衡の下では、どのプレーヤーも戦略を変更する誘因を持たない。
ナッシュ均衡は必ずしもパレート効率的ではない。その代表例が囚人のジレンマである。
https://ja.wikipedia.org/wiki/ナッシュ均衡
どゆことなの
>>33
詳しく説明する
ゲームの参加者を合理的な人間であると仮定する
ここで合理的とは「生を求め死を避ける」こととする
つまり、死ぬよりは部屋から出られない方を選ぶってこった
そうすると利得は
大金をもらって解放される…+10
解放される…0
一生部屋から出られない…-5
死ぬ…-10
って感じで設定できるだろ
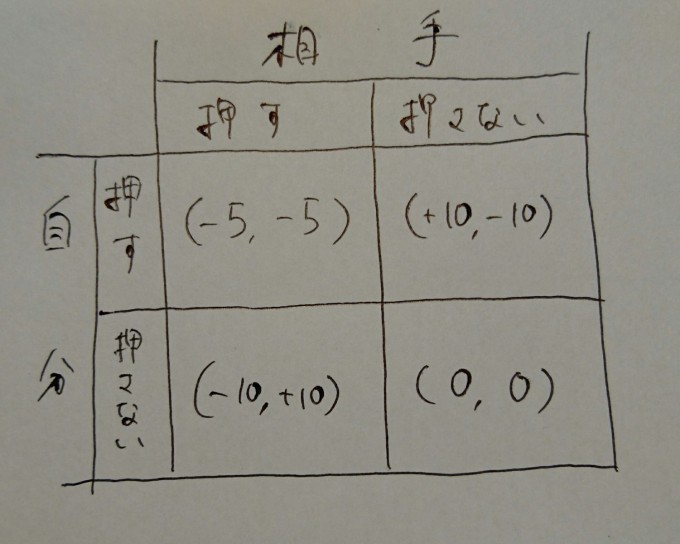
そうすると、このように表にできる
表の見方は(自分の利得、相手の利得)ね
・相手が押す場合
→自分も押す…-5
→押さない…-10
・相手が押さない場合
→自分は押す……+10
→押さない…0
よって「押す」を選ばなきゃどうしても損するだけ
つまり2人とも合理的であれば、結局「部屋から出られない」という結果になるというわけ
明からに、2人とも解放される結果の方がこれよりいいに決まってるのにな
>>36
この表の右下の(0、0)っいうのがナッシュ均衡と呼ばれる
ナッシュ均衡とは、
「他のプレイヤーの戦略を所与とした時、全てのプレイヤーが最善の戦略を選択しているような組み合わせ」
のことで、この組み合わせではどのプレイヤーも戦略を変える誘引をもたない
米ソ冷戦時代の軍拡競争を説明する時にもこのモデルが使われたりする
実は一昨日のセンター試験の政経でこれが出たらしい
センターでゲーム理論か
なかなか
まぁ実際には「死ぬ方がいい」とか言う天邪鬼もいるから
上の表は現実世界では必ずしも妥当ではないけどね
センター政経でゲーム理論とか前からやってるぞ
>>40
まぁリード文で説明してたら高校生にもわかんない内容じゃないしね
ていうかVIPでよくお前らがお薦めする映画『ビューティフルマインド』
あれがナッシュ均衡を発見したジョン・ナッシュの半生を描いた映画なんだぞ
あの映画観てるならナッシュ均衡も知っとけ
もう誰も見てないかな
じゃあ付き合ってくれてありがとう
ばいばい
俺は一生飯が出るって言う点で最悪出られなくてもまあ良いなって思ったわ
○押さない→出られるor死ぬ
○押す→相方が俺の行動で死んだと一生悔やむ代わりに大金を得る
○押した後相方に「押すから」と言う→相方は押さざるを得ないから仲良く個室生活スタート
万が一そんな生活する位なら死を選ぶと相方が押さなかった場合大金を得るがそれは相方が選んだ死であるので黙って押すより罪悪感が少ない
○押した後相方に「押さないから」という→大金を得たら罪悪感MAX、出れなかったらまあそうだよなwと諦める
○押さないで相方に「押すから」と言う→自殺願望者、自分が死んだ場合は相方に少なからず罪悪感を残す鬼畜
死ななかった場合物語が始まる
○押さないで相方に「押さないから」と言う→責任を全て相方に擦り付ける卑怯者、死んだら相方を直前に怨むだろう
死ななかったとしてもジャッジまでの間に相方が押さないかと堂々巡りするだろう
>>44
すげぇ緻密な分析だなぁ
人間の心理をよく考えてる
ジョンナッシュタクシーで死んじゃったね
>>1は何専攻なの
>>46
おれは生物系だよ
ゲーム理論はちょっとかじっただけで全然詳しくないよ